
abstract algebra - Why is commutativity optional in multiplication for rings? - Mathematics Stack Exchange

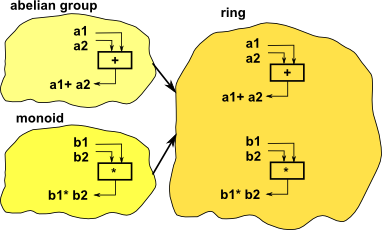
SOLVED: The Ring Axioms The set R is closed under addition and multiplication, meaning that for all %, Y € R,x +y € Rand x Y € R Addition is associative, meaning

Z-module reasoning: an equality-oriented proving method with built-in ring axioms: Journal of the ACM: Vol 40, No 3
LECTURE 26 RING SCHEMES; THE WITT SCHEME §0. Outline In section 1, the viewpoint of the ring schemes is introduced, with some b

SOLVED: Definition 5.4 (Axioms of Ring) . A ring is a set R of elements on which two binary operations, addition (+ R) and multiplication ( R), are defined that satisfy the
THE ORIGINS OF THE DEFINITION OF ABSTRACT RINGS Contents 1. Introduction 5 2. Postulational Analysis in the USA 6 3. Theory of p


![summarizes the axioms that define groups, rings, and field[Sta05] | Download Scientific Diagram summarizes the axioms that define groups, rings, and field[Sta05] | Download Scientific Diagram](https://www.researchgate.net/publication/312277471/figure/fig1/AS:449838375542784@1484261234519/1-summarizes-the-axioms-that-define-groups-rings-and-fieldSta05.png)



![summarizes the axioms that define groups, rings, and field[Sta05] | Download Scientific Diagram summarizes the axioms that define groups, rings, and field[Sta05] | Download Scientific Diagram](https://www.researchgate.net/profile/Qasim-Hussein/publication/278675750/figure/fig1/AS:614212300701716@1523451032614/1-summarizes-the-axioms-that-define-groups-rings-and-fieldSta05_Q640.jpg)






